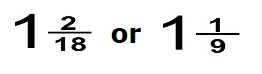Fractions
Understanding fractions can be easy if you look at it from a graphical point of view. For example if you have a whole apple pie and you need to share 2/3 of it. How would you do that?
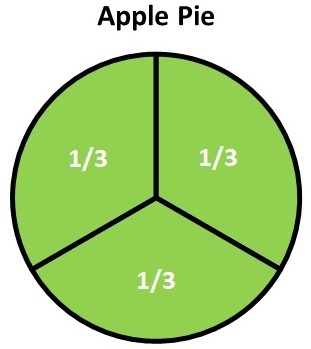
If you share the 2/3 of the pie only 1/3 is left.
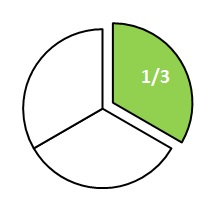
A fraction consists of a numerator (top number) and a denominator (bottom number). If you look at the 2/3 of the apple pie the numerator is 2 and the denominator is 3.
Whole Numbers
In the above example the fraction 3/3 is equal to one whole apple pie. The fraction 6/5 is known as an improper fraction because the top number is bigger than the bottom number. How many whole numbers do you think there are in the fraction 6/5?
Divide 6 by 5 = 1 1/5
If you have to do any calculations with whole numbers you should convert them to fractions.
Example:
1 1/3 × 1 2/4 = 4/3 × 6/4
Fractions in Simplest Form
Fractions can be written in simplest form. We need to know the common factor number that can be divided into both the top and bottom number exactly.
Example 1
The fraction 18/27 has a common factor 9
Top Number: 18/9 = 2
Bottom Number: 27/9 = 3
Simplest Form: 2/3
Example 2
The fraction 12/24 has a common factor 12
Top Number: 12/12 = 1
Bottom Number: 24/12 = 2
Simplest Form: 1/2
Addition
4/3 + 2/6 = ?
The first rule is to make the bottom numbers the same.
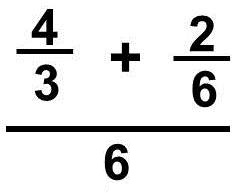
Start with the first fraction 4/3:
- 3 goes into 6 = 2
- Multiply the 2 with the top
number2 × 4 = 8 - 4/3=8/6
Second fraction 2/6:
- 6 goes into 6 = 1
- Multiply the 1 with the top
number 1 × 2 = 2 - 2/6=2/6 no change
Now it is easier to add up the fractions.
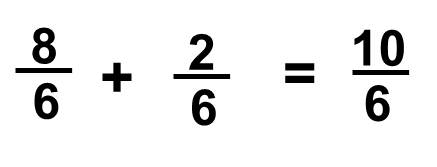
Note:10/6 is known as an improper fraction because we can simplify it.
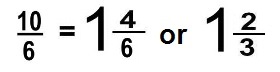
A proper fraction would be 2/3 because you cannot simplify it.
Subtraction
2/3 - 3/9 = ?
For subtraction we use the same rule as addition; make the bottom numbers the same. The number that would go into the denominators 3 and 9 would be 9.
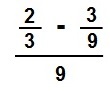
Start with the first fraction 2/3:
- 3 goes into 9 = 3
- Multiply the 3 with the top
number 3 × 2 = 6 - 2/3=6/9
Second fraction 3/9:
- 9 goes into 9 = 1
- Multiply the 1 with the top
number 1 × 3 = 3 - 3/9=3/9 no change
Now it is easier to subtract the fractions.
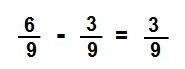
We can simplify 3/9 to 1/3, which is a proper fraction.
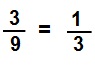
Multiplication
6/8 x 3/2 = ?
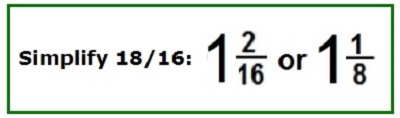
The rule is different for multiplication. Multiply the top numbers 6 x 3 =18 and then multiply the bottom numbers 8 x 2 = 16.
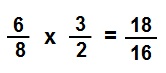
Division
4/6 ÷ 3/5 = ?
In division the numbers for the second fraction 3/5 have to be reversed, before we multiply the numbers.
|
Before 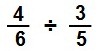
|
After 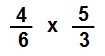
|
Multiply the top numbers 4 × 5 = 20 and the bottom numbers 6 × 3 =18.
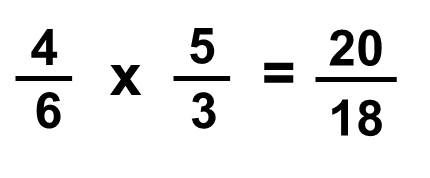
We can simplify 20/18 (improper fraction):