Factors
We need to understand prime numbers and factors before we can find the prime factors of a number.
Prime Numbers
A prime number can only be divided by itself and 1. A prime number does not have any remainders. The table below shows prime numbers up to 60
| Prime Numbers | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 5 | 7 | 9 | 11 |
| 17 | 19 | 23 | 29 | 31 | 37 | 39 |
| 41 | 43 | 47 | 51 | 53 | 57 | 59 |
Factors
Factors are whole numbers that can be multiplied together to equal a product.
Example 1
2 × 8 = 16
2 and 8 are factors and
16 is the product.
Example 2
3 × 5 = 15
3 and 5 are factors and
15 is the product.
Factors of a Number
Now we are going to find the factors of a number.
Factors of 4
1 × 4 = 4
2 × 2 = 4
Factors of 4 are: 1,2 and 4
Factors of 6
1 × 6 = 6
2 × 3 = 6
Factors of 6 are: 1,2,3 and 6
Factors of 8
1 × 8 = 8
2 × 4 = 8
Factors of 8 are: 1,2,4 and 8
Factors of 9
1 × 9 = 9
3 × 3 = 9
Factors of 9 are: 1,3 and 9
Prime Factors of a Number
We know what prime numbers and factors are, so now we are going to find the prime factors of a number using two different methods.
Example 1: Prime Factors of 18
Method 1
- Divide 18/2 = 9
9 is not a prime number
so we continue dividing - Divide 9/3 = 3
3 is the final prime number - The prime factors of 18:
2 x 3 x 3 = 18
Method 2
This is the tree method.
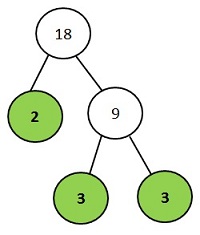

Use the tree method for finding the prime factors for large numbers.
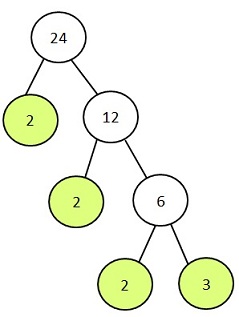
Example 2: Prime Factors of 24
- Divide 24/2 = 12
12 is not a prime number
so we continue dividing - Divide 12/2 = 6
6 is not a prime number
so we continue dividing - Divide 6/2 = 3
3 is the final prime number - The prime factors of 24:
2 x 2 x 2 x 3 = 24
This is the tree method.

Lowest Common Multiple (LCM)
To find the LCM of 6 and 8 we need to know the mutiples of 6 and 8 (times table for 6 and 8).
Multiples of 6
6, 12, 18, 24, 30, 36, 42,48
Multiples of 8
8, 16, 24, 32, 40, 48, 56
We can see the numbers 24 and 48 appear in both the multiples. The smallest number is 24 so the LCM is 24.
Tree Method (LCM)
We can also use the tree method to find the LCM of two numbers.
Finding the LCM of 6 and 8 using the tree method:
Step 1: Find the prime factors of 6 and 8.
Prime Factors of 6
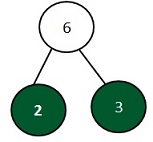

Prime Factors of 8
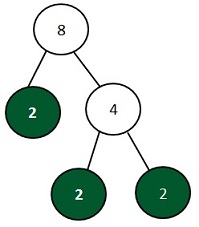
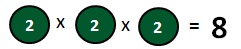
Step 2: Now we have to find the tree with the most 2s and 3s.
Prime factors of 6 are 2 x 3
Prime factors of 8 are 2 x 2 x 2
- The tree with the most 2s is tree 8.
It has: 2 x 2 x 2 - The only tree with a 3 is tree 6.
It has: 1 x 3 - Multiply the numbers: 2 x 2 x 2 x 3 = 24
LCM = 24
Highest Common Factor (HCF)
To find the HCF of 24 and 36 we need to know the factors of 24 and 36.
Factors of 24
1 x 24
2 x 12
3 x 8
4 x 6
Factors of 24:
1,2,3,4,6,8,12,24
Factors of 36
1 x 36
2 x 18
3 x 12
4 x 9
6 x 6
Factors of 36:
1,2 ,3,4,6,9,12,18,36
The numbers common in both of the lists are: 1,2,3,4,6 and 12. The hightest common factor is 12.
HCF= 12
Tree Method
We can also use the tree method to find the HCF of 24 and 36.
Step 1: Find the prime factors
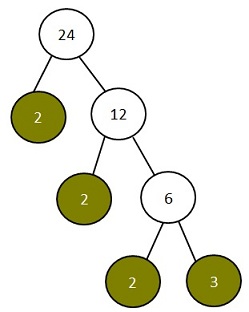
Prime Factors of 24

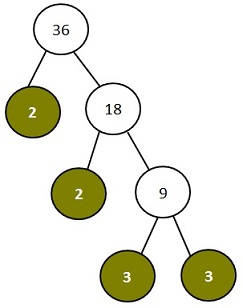
Prime Factors of 36

Step 2: Look for the common factors.
The common factors of 24 and 36 are coloured in green.
| 2 | x | 2 | x | 2 | x | 3 | = | 24 |
| 2 | x | 2 | x | 3 | x | 3 | = | 36 |
Step 3: Mutlply the common factors from one of the list to find the HCF.
2 x 2 x 3 = 12
HCF= 12