Decimals
A decimal point separates whole numbers from numbers with value less than 1.
Example: 3.232
| Thousands | Hundreds | Tens | Units | Tenths | Hundredths | Thousandths |
| 3 | 2 | 3 | 2 |
The number 3, which is to the right, is a whole number and the numbers to the left are as follows:
- Tenths = 2/10
- Hundredths = 3/100
- Thousandths = 2/1000
More Examples!
Example 1
6.22
Six is a whole number (6 units) and .22 is less than one
2/10 + 2/100 = 22/100.
| Th | H | T | U | 1/10 | 1/100 | 1/1000 |
| 6 | 2 | 2 |
Example 2
56.134
56 is a whole number (5 tens and 6 units) and .134 is less than one
1/10 + 3/100 + 4/1000 = 134/1000.
| Th | H | T | U | 1/10 | 1/100 | 1/1000 |
| 5 | 6 | 1 | 3 | 4 |
Example 3
734.356
734 is a whole number (7 hundreds,3 tens and 4 units) and .356 is less than one
3/10 + 5/100 + 6/1000 = 356/1000.
| Th | H | T | U | 1/10 | 1/100 | 1/1000 |
| 7 | 3 | 4 | 3 | 5 | 6 |
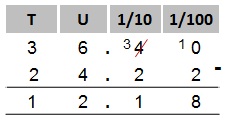
Addition
We have to align the decimal points, before we add up.
| U | 1/10 | |
|---|---|---|
| 2. | 4 | + |
| 5. | 1 | |
| 7. | 5 | |
| U | 1/10 | 1/100 | |
|---|---|---|---|
| 4. | 2 | 9 | |
| 2. | 3 | 8 | + |
| 6. | 6 | 7 | |
| 1 | |||
| T | U | 1/10 | 1/100 | |
|---|---|---|---|---|
| 1 | 6. | 5 | 2 | |
| 3 | 5. | 2 | 4 | + |
| 5 | 1. | 7 | 6 | |
| 1 | ||||
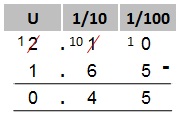
Subtraction
Just like addition, we have to align the decimal points.
Multiplication
Example 1: 2.5 x 3 = ?
1. Remove the decimal point
and multiply as normal.
Note! 2.5 has only one number after the decimal
point.
| 2 5 | x |
| 3 | |
| 7 5 | |
| 1 |
2. Add a decimal point after the 7.
Hence, the answer has one number after
the
decimal point.
Answer=7.5
Example 2: 4.2 x 2.1=?
1. Remove the decimal points and multiply
as normal.
Note! 4.2 has one number
after the decimal
point and 2.1 has one number after the decimal
point 1+1=2.
| 4 | 2 | x | |
| 2 | 1 | ||
| 4 | 2 | ||
| 8 | 4 | 0 | |
| 8 | 8 | 2 | |
2. The answer should have two numbers
after the decimal point. Hence, add the
decimal point after the 8.
Answer=8.82
Multiply by 10
If we multiply by 10 we move the decimal point one place to the right.
Example 1
3.5 × 10= ?
Answer=35
Example 2
4.678 × 10= ?
Answer=46.78
Example 3
45.43 × 10= ?
Answer=454.3
Multiply by 100
If we multiply by 100 we move the decimal point two places to the right.
Example 1
4.56 x 100= ?
Answer=456
Example 2
13.23 x 100= ?
Answer=1323
Example 3
3.384 x 100= ?
Answer=338.4
Multiply by 1000
If we multiply by 1000 we move the decimal point three places to the right.
Example 1
0.64 x 1000= ?
Answer=640
Example 2
1.230 x 1000= ?
Answer=1230
Example 3
7.254 x 1000= ?
Answer=7254
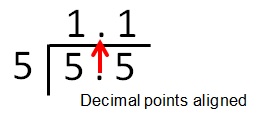
Division
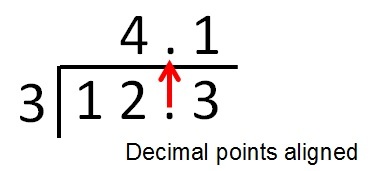
Divide as normal but the decimal point for the answer should be aligned to the decimal point inside the division bracket.
Example 1
Divide 5.5 by 5
Example 2
Divide 12.3 by 3
In the above division we divided decimal numbers by whole numbers. Now we are going to divide decimal numbers by decimal numbers.
Example 1
7.5 ÷ 2.5 = ?
- Multiply both the numbers by 10 to make it easier for us to divide.
7.5 x 10 = 75
2.5 x 10 = 25 - Divide 75 by 25
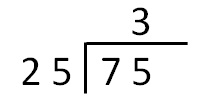
Dividing 75 by 25 is the same as dividing 7.5 by 2.5. Therefore the answer is 3
.Example 2
1.4412 ÷ 0.12=?
- Multiply both the numbers by 100 to make it easier for us to divide.
1.4412 x 100 = 144.12
0.12 x 100 = 12 - Divide 144.12 by 12.
It helps if you know
your 12 times table!
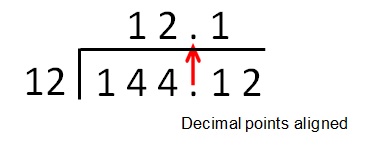
Dividing 144.12 by 12 is the same as dividing 1.4412 by 0.12 Therefore the answer is 12.1.
Divide by 10
If we divide by 10 we move the decimal point one place to the left.
Example 1
44 ÷ 10= ?
Answer=4.4
Example 2
67.42 ÷ 10= ?
Answer=6.742
Example 3
4.54 x 10= ?
Answer=0.454
Divide by 100
If we divide by 100 we move the decimal point two places to the left.
Example 1
236.2 ÷ 100= ?
Answer=2.362
Example 2
12.34 ÷ 100= ?
Answer=0.1234
Example 3
3.45 ÷ 100= ?
Answer=0.0345
Divide by 1000
If we divide by 1000 we move the decimal point three places to the left.
Example 1
435.2 ÷ 1000= ?
Answer=0.4352
Example 2
12382.5 ÷= ?
Answer=12.3825
Example 3
5325.34 ÷= ?
Answer=5.32534
Recurring Decimal Number
A recurring decimal number is a number that is continously repeated. For example dividing 2 by 3 will give us a continous repeated decimal number 6.
2/3 = 0.6666666666666
0.66666666666 can be shortened to
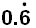
Decimals to Percentages
Multiply the decimal number by 100 for example 0.5 x 100= 50%
0.546 x 100 = 54.6%
0.035 x 100 = 3.5%
To convert the percentages back to decimals divide by 100.
Fractions to Decimals
2/5 means 2 divide by 5
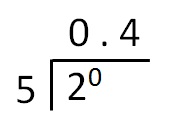
2/5 = 0.4
Decimals to Fractions
0.4 means 4/10
.| Th | H | T | U | 1/10 | 1/100 | 1/1000 |
| 4 |
We can say 4/10 equals 2/5 by dividing the top and bottom numbers by 2.
0.75 means 7/10 + 5/100 = 75/100
| Th | H | T | U | 1/10 | 1/100 | 1/1000 |
| 7 | 5 |
We can say 75/100 = 3/4 by dividing the top and bottom number by 25.
Whole Numbers
Whole numbers can be converted into fractions. For example we know 0.4 means 4/10 so 1.4 would mean 10/10 + 4/10 = 14/10.
More Examples!
2.4 in fractions means 20/10 + 4/10 = 24/10
3.6 in fractions means 30/10 + 6/10 = 36/10
1.75 in fractions means 100/100 + 75/100 = 175/100
2.75 in fraction means 200/100 + 75/100 = 275/100